| Classwise Concept with Examples | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 2 Relations and Functions (Concepts)
Building directly upon the foundational language of sets, this chapter introduces two pivotal mathematical concepts – Relations and Functions – which are essential for describing connections and dependencies between quantities. While sets deal with collections, relations and functions allow us to model the intricate ways elements from one set can be associated with elements of another, forming the bedrock for calculus, algebra, and virtually all areas where relationships are analyzed. We begin by formalizing the idea of an Ordered Pair, denoted as $(a, b)$, where, unlike elements within a set, the order in which the elements appear is critically important. This concept is fundamental for representing coordinates and defining more complex structures.
The first structure we build is the Cartesian Product of two non-empty sets, $A$ and $B$. Denoted as $A \times B$, this product is defined as the set of all possible ordered pairs $(a, b)$ such that the first element $a$ belongs to set $A$ ($a \in A$) and the second element $b$ belongs to set $B$ ($b \in B$). Mathematically, $A \times B = \{(a, b) | a \in A \text{ and } b \in B\}$. Think of this as creating the universe of all potential pairings between elements of $A$ and $B$. From this universe, we define a Relation $R$ from set $A$ to set $B$ as any subset of the Cartesian product $A \times B$ ($R \subseteq A \times B$). A relation essentially selects specific ordered pairs from $A \times B$ that satisfy a particular rule or condition, thereby describing a link or connection between elements. We identify key components associated with a relation $R$: the Domain (the set of all first elements 'a' that appear in the ordered pairs of $R$), the Range (the set of all second elements 'b' that appear in the ordered pairs of $R$), and the Codomain (which is always the entire set $B$). Relations can be represented visually using arrow diagrams, or explicitly using roster form or set-builder notation.
The core focus then narrows to a very special and ubiquitous type of relation known as a Function. A function $f$ from a non-empty set $A$ to a non-empty set $B$, denoted symbolically as $f: A \rightarrow B$, is a specific rule or correspondence that associates each element of set $A$ with exactly one element of set $B$. This is the defining characteristic: every element in the domain $A$ must have one, and only one, 'image' or corresponding element in the codomain $B$. We learn to rigorously distinguish functions from mere relations by checking these two conditions. The terms Domain (set $A$), Codomain (set $B$), and Range (the set of all actual image values in $B$, which is a subset of the codomain, Range $\subseteq$ Codomain) are precisely defined for functions.
We then explore several important types of real-valued functions (where the domain and range are subsets of the set of real numbers, $\mathbb{R}$), examining their definitions, characteristic graphs, domains, and ranges. Key examples include:
- The Identity Function: $f(x) = x$
- The Constant Function: $f(x) = c$, where $c$ is a constant.
- Polynomial Functions: $f(x) = a_0 + a_1x + a_2x^2 + \dots + a_nx^n$
- Rational Functions: $f(x) = \frac{P(x)}{Q(x)}$, where $P(x)$ and $Q(x)$ are polynomials and $Q(x) \neq 0$.
- The Modulus Function: $f(x) = |x|$ (absolute value).
- The Signum Function.
- The Greatest Integer Function: $f(x) = [x]$ or $\lfloor x \rfloor$ (largest integer less than or equal to $x$).
Finally, the chapter investigates the Algebra of Real Functions. Just as we can perform arithmetic operations on numbers, we can define operations on functions. Given two real functions $f$ and $g$ with suitable domains, we define:
- Sum: $(f+g)(x) = f(x) + g(x)$
- Difference: $(f-g)(x) = f(x) - g(x)$
- Product: $(fg)(x) = f(x)g(x)$
- Quotient: $(\frac{f}{g})(x) = \frac{f(x)}{g(x)}$, provided $g(x) \neq 0$.
Ordered Pair
In mathematics, when we talk about a pair of objects or numbers, the order in which they are presented can sometimes be important. An ordered pair is a fundamental concept that represents a collection of two elements where the order of the elements is significant.
An ordered pair is written by enclosing the two elements within parentheses and separating them by a comma, like $(a, b)$. In the ordered pair $(a, b)$, $a$ is called the first element or first component, and $b$ is called the second element or second component.
The key characteristic of an ordered pair is that the order matters. Unlike a set $\{a, b\}$ where $\{a, b\} = \{b, a\}$, the ordered pair $(a, b)$ is generally not the same as the ordered pair $(b, a)$.
For example, in coordinate geometry, the ordered pair $(2, 3)$ represents a specific point on a plane (2 units along the x-axis, 3 units along the y-axis), which is different from the point $(3, 2)$ (3 units along the x-axis, 2 units along the y-axis).
The only time $(a, b) = (b, a)$ is when the first and second elements are identical, i.e., when $a = b$. In this case, the ordered pair is of the form $(a, a)$.
Equality of Ordered Pairs:
Two ordered pairs are considered equal if and only if their corresponding elements are equal. This means the first component of the first ordered pair must equal the first component of the second ordered pair, AND the second component of the first ordered pair must equal the second component of the second ordered pair.
Symbolically, two ordered pairs $(a, b)$ and $(c, d)$ are equal if and only if:
$(a, b) = (c, d) \iff a = c \text{ and } b = d$
... (1)
This definition is crucial for solving problems involving unknown values in ordered pairs.
Example 1. Find the values of $x$ and $y$ if $(x+2, y-3) = (4, 1)$.
Answer:
Given:
The equality of two ordered pairs:
$(x+2, y-3) = (4, 1)$
To Find:
Values of the variables $x$ and $y$.
Solution:
According to the definition of equality of ordered pairs (Equation 1), two ordered pairs are equal if and only if their corresponding first components are equal and their corresponding second components are equal.
Equating the first components:
$x+2 = 4$
To find the value of $x$, subtract 2 from both sides of the equation:
$x = 4 - 2$
$x = 2$
Equating the second components:
$y-3 = 1$
To find the value of $y$, add 3 to both sides of the equation:
$y = 1 + 3$
$y = 4$
Thus, the values of $x$ and $y$ are 2 and 4 respectively.
The final answer is $\textbf{x = 2, y = 4}$.
Ordered Triples and Ordered $n$-tuples:
The concept of ordered pairs can be extended to ordered collections of more than two elements where the order is important.
Ordered Triple:
An ordered triple is a collection of three elements in a specific order, written as $(a, b, c)$. Here, $a$ is the first element, $b$ is the second, and $c$ is the third. For example, $(1, 2, 3)$ is different from $(3, 2, 1)$.
Two ordered triples $(a, b, c)$ and $(d, e, f)$ are equal if and only if their corresponding components are equal:
$(a, b, c) = (d, e, f) \iff a = d, b = e, \text{ and } c = f$.
Ordered triples are used, for instance, to represent points in three-dimensional space, such as $(x, y, z)$.
Ordered $n$-tuple:
In general, an ordered $n$-tuple is a sequence or list of $n$ elements $(a_1, a_2, ..., a_n)$ where the order is specifically defined. Here, $a_1$ is the first element, $a_2$ is the second, and so on, up to $a_n$ as the $n$-th element.
Two ordered $n$-tuples $(a_1, a_2, ..., a_n)$ and $(b_1, b_2, ..., b_n)$ are equal if and only if $a_i = b_i$ for all $i = 1, 2, ..., n$.
Ordered $n$-tuples are fundamental in various areas of mathematics and computer science, such as representing vectors, points in $n$-dimensional space, or rows in a database table.
Cartesian Product of Two Sets
Building upon the concept of ordered pairs, we now define an operation that combines two sets to form a new set consisting of all possible ordered pairs formed by taking the first element from the first set and the second element from the second set. This operation is called the Cartesian product.
Given two non-empty sets $A$ and $B$, the Cartesian product of $A$ and $B$, denoted by $A \times B$, is the set of all possible ordered pairs $(a, b)$ where the first component $a$ is an element of set $A$, and the second component $b$ is an element of set $B$.
Symbolic Definition:
The Cartesian product $A \times B$ is defined formally using set-builder notation as:
$A \times B = \{ (a, b) : a \in A, b \in B \}$
... (1)
The symbol '$\times$' used here is read as "cross".
Examples of Cartesian Product:
Let's look at some examples to understand how to form the Cartesian product of sets.
1. If $A = \{a, b\}$ and $B = \{1, 2, 3\}$.
To find $A \times B$, we form all ordered pairs $(a, b)$ where $a$ is from $A$ and $b$ is from $B$. Take the first element from $A$ (which is $a$) and pair it with each element of $B$: $(a, 1), (a, 2), (a, 3)$. Take the second element from $A$ (which is $b$) and pair it with each element of $B$: $(b, 1), (b, 2), (b, 3)$. The set of all these ordered pairs is $A \times B$.
$A \times B = \{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) \}$
Now, let's find $B \times A$. We form all ordered pairs $(b, a)$ where $b$ is from $B$ and $a$ is from $A$. Take the first element from $B$ (which is 1) and pair it with each element of $A$: $(1, a), (1, b)$. Take the second element from $B$ (which is 2) and pair it with each element of $A$: $(2, a), (2, b)$. Take the third element from $B$ (which is 3) and pair it with each element of $A$: $(3, a), (3, b)$. The set of all these ordered pairs is $B \times A$.
$B \times A = \{ (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) \}$
Comparing $A \times B$ and $B \times A$, we see they contain different ordered pairs (e.g., $(a, 1)$ is in $A \times B$ but not in $B \times A$). This confirms that in general, $A \times B \neq B \times A$. The Cartesian product is commutative only if $A = B$ or if one of the sets is empty.
2. If $A = \{ \text{Red, Blue} \}$ and $B = \{ \text{Shirt, Trousers} \}$.
This example could represent possible outfit combinations based on colour and type of clothing. $A \times B = \{ (\text{Red, Shirt}), \ $$ (\text{Red, Trousers}), \ $$ (\text{Blue, Shirt}), \ $$ (\text{Blue, Trousers}) \}$. Each ordered pair represents a distinct combination.
Cartesian Product of Three Sets:
The concept of the Cartesian product can be extended to more than two sets. The Cartesian product of three sets $A, B,$ and $C$ is the set of all possible ordered triples $(a, b, c)$ where the first element $a$ is from set $A$, the second element $b$ is from set $B$, and the third element $c$ is from set $C$.
Symbolic Definition:
$A \times B \times C = \{ (a, b, c) : a \in A, b \in B, c \in C \}$
... (2)
This results in a set of ordered triples. This concept can be generalized to the Cartesian product of $n$ sets, which results in a set of ordered $n$-tuples.
Properties of Cartesian Product:
The Cartesian product has several important properties related to the sets involved and their cardinalities.
1. Non-emptiness: If both set $A$ and set $B$ are non-empty, then their Cartesian product $A \times B$ is also a non-empty set. This is because if $A$ has at least one element $a$ and $B$ has at least one element $b$, then the ordered pair $(a, b)$ will be an element of $A \times B$.
2. Involvement of Empty Set: If either set $A$ or set $B$ (or both) is the empty set ($\emptyset$), then their Cartesian product is the empty set.
$A \times \emptyset = \emptyset$
$\emptyset \times B = \emptyset$
$\emptyset \times \emptyset = \emptyset$
This is because to form an ordered pair $(a, b)$ with $a \in A$ and $b \in B$, both $A$ and $B$ must contain at least one element. If one is empty, no such pair can be formed.
3. Cardinality of Cartesian Product: If $A$ and $B$ are finite sets, then their Cartesian product $A \times B$ is also a finite set. The number of elements in $A \times B$ is equal to the product of the number of elements in set $A$ and the number of elements in set $B$.
$n(A \times B) = n(A) \times n(B)$
... (3)
This formula stems directly from the process of forming ordered pairs: for each element in $A$, you can pair it with $n(B)$ different elements from $B$. If $A$ has $n(A)$ elements, and each can be paired with $n(B)$ elements, the total number of pairs is $n(A) \times n(B)$.
Similarly, for the Cartesian product of three finite sets $A, B,$ and $C$, the cardinality is:
$n(A \times B \times C) = n(A) \times n(B) \times n(C)$
... (4)
This can be extended to the Cartesian product of $n$ finite sets.
Example 1. If $A = \{1, 2\}$ and $B = \{a, b, c\}$, find $n(A \times B)$ and list the elements of $A \times B$.
Answer:
Given:
Set $A = \{1, 2\}$
Set $B = \{a, b, c\}$
To Find:
The number of elements in the Cartesian product $A \times B$, i.e., $n(A \times B)$.
The set of elements in the Cartesian product $A \times B$.
Solution:
First, let's find the number of elements in each set:
$n(A) = 2$
$n(B) = 3$
Using the formula for the cardinality of the Cartesian product (Formula 3):
$n(A \times B) = n(A) \times n(B)$
Substitute the values of $n(A)$ and $n(B)$:
$n(A \times B) = 2 \times 3$
$n(A \times B) = 6$
There are 6 elements in the Cartesian product $A \times B$.
Now, let's list the elements of $A \times B$. These are all ordered pairs $(x, y)$ where $x \in A$ and $y \in B$. We systematically pair each element of $A$ with each element of $B$:
From element $1 \in A$: $(1, a), (1, b), (1, c)$
From element $2 \in A$: $(2, a), (2, b), (2, c)$
Collect all these ordered pairs into a set:
$A \times B = \{ (1, a), (1, b), (1, c), (2, a), (2, b), (2, c) \}$
The final answer is $\textbf{n(A} \times \textbf{B) = 6}$ and $\textbf{A} \times \textbf{B = } $$ \{(1, a), (1, b), \ $$ (1, c), \ $$ (2, a), \ $$ (2, b), (2, c)\}$.
The Cartesian product is fundamental in defining coordinates for geometrical spaces. For example:
- The set of points in a two-dimensional Cartesian plane can be represented as the Cartesian product of the set of real numbers with itself: $\mathbb{R} \times \mathbb{R}$, often denoted as $\mathbb{R}^2$. An element of $\mathbb{R}^2$ is an ordered pair $(x, y)$ where $x, y \in \mathbb{R}$.
- The set of points in three-dimensional space can be represented as the Cartesian product of the set of real numbers with itself three times: $\mathbb{R} \times \mathbb{R} \times \mathbb{R}$, often denoted as $\mathbb{R}^3$. An element of $\mathbb{R}^3$ is an ordered triple $(x, y, z)$ where $x, y, z \in \mathbb{R}$.
This connection between sets and geometry highlights the power and applicability of set theory.
Relations
In our everyday language, the word "relation" signifies a connection or link between two entities. In mathematics, the concept of a relation between two sets formalizes this idea of a connection between the elements of those sets.
Given two non-empty sets $A$ and $B$, a relation $R$ from set $A$ to set $B$ is defined as any subset of the Cartesian product $A \times B$. Recall that $A \times B$ is the set of all possible ordered pairs $(a, b)$ where $a \in A$ and $b \in B$. A relation $R$ simply selects some of these ordered pairs based on a specific rule or condition.
If $R$ is a relation from $A$ to $B$, then by definition, $R \subseteq A \times B$.
If a specific ordered pair $(a, b)$ is an element of the relation $R$ (i.e., $(a, b) \in R$), we say that "$a$ is related to $b$ by the relation $R$". This can also be written in shorthand notation as $a R b$.
If an ordered pair $(a, b)$ is not an element of the relation $R$ (i.e., $(a, b) \notin R$), we say that "$a$ is not related to $b$ by the relation $R$".
The set $A$ is called the domain of the relation (or sometimes the set of inputs), and the set $B$ is called the codomain (or the set of possible outputs).
Number of Relations:
Given two finite sets $A$ and $B$, we can determine the total number of possible relations that can be defined from $A$ to $B$.
Let the number of elements in set $A$ be $n(A) = p$.
Let the number of elements in set $B$ be $n(B) = q$.
The Cartesian product $A \times B$ contains all possible ordered pairs $(a, b)$ with $a \in A$ and $b \in B$. The number of such ordered pairs is given by the cardinality of the Cartesian product:
$n(A \times B) = n(A) \times n(B) = pq$.
A relation from $A$ to $B$ is defined as any subset of $A \times B$. From our study of sets, we know that if a set has $N$ elements, the total number of possible subsets of that set is $2^N$ (this is the cardinality of the power set). In this case, the set is $A \times B$, and it has $pq$ elements. Therefore, the number of subsets of $A \times B$ is $2^{pq}$.
Each subset of $A \times B$ corresponds to a unique relation from $A$ to $B$. Thus, the total number of possible relations from set $A$ to set $B$ is $2^{pq}$.
Number of relations from $A$ to $B = 2^{n(A) \times n(B)}$
... (1)
This formula gives the total count of all possible ways to relate elements of $A$ to elements of $B$, including relations that might seem trivial or meaningless in a specific context.
Example 1. Let $A = \{1, 2\}$ and $B = \{3, 4\}$. Find the number of relations from $A$ to $B$. List one relation $R_1$ from $A$ to $B$ such that $a R_1 b$ if $a < b$.
Answer:
Given:
Set $A = \{1, 2\}$
Set $B = \{3, 4\}$
Relation rule: $a R_1 b$ if $a < b$, where $a \in A$ and $b \in B$.
To Find:
Total number of relations from $A$ to $B$.
List the ordered pairs belonging to the relation $R_1$.
Solution:
First, find the number of elements in sets $A$ and $B$:
$n(A) = 2$
$n(B) = 2$
The total number of possible relations from $A$ to $B$ is $2^{n(A) \times n(B)}$.
Number of relations $= 2^{2 \times 2} = 2^4$
$2^4 = 2 \times 2 \times 2 \times 2 = 16$
So, there are 16 possible relations from set $A$ to set $B$.
Now, let's list the ordered pairs in the relation $R_1$, which is defined by the condition $a < b$, where $a \in A$ and $b \in B$. We need to check each ordered pair in the Cartesian product $A \times B$ against this condition.
First, let's list the elements of $A \times B$:
$A \times B = \{ (1, 3), (1, 4), (2, 3), (2, 4) \}$
Now, check the condition $a < b$ for each pair $(a, b)$ in $A \times B$:
- For the pair $(1, 3)$: Is $1 < 3$? Yes. So, $(1, 3) \in R_1$.
- For the pair $(1, 4)$: Is $1 < 4$? Yes. So, $(1, 4) \in R_1$.
- For the pair $(2, 3)$: Is $2 < 3$? Yes. So, $(2, 3) \in R_1$.
- For the pair $(2, 4)$: Is $2 < 4$? Yes. So, $(2, 4) \in R_1$.
All ordered pairs in $A \times B$ satisfy the condition $a < b$. Therefore, the relation $R_1$ consists of all elements of $A \times B$.
$R_1 = \{ (1, 3), (1, 4), (2, 3), (2, 4) \}$
The final answer is $\textbf{16}$ relations and $\textbf{R}_1 = \{(1, 3), (1, 4), (2, 3), (2, 4)\}$.
Special Types of Relations:
Among the total possible relations from $A$ to $B$, some are special cases.
1. Empty Relation (Void Relation): The empty set $\emptyset$ is a subset of any set, including $A \times B$. Therefore, the empty set is always a relation from $A$ to $B$. This relation is called the empty relation because it contains no ordered pairs, meaning no element of $A$ is related to any element of $B$.
$R = \emptyset \subseteq A \times B$
2. Universal Relation: The Cartesian product $A \times B$ itself is a subset of $A \times B$. Thus, $A \times B$ is a relation from $A$ to $B$. This relation is called the universal relation because it contains all possible ordered pairs, meaning every element of $A$ is related to every element of $B$.
$R = A \times B$
When the relation is defined from a set $A$ to itself (i.e., $R \subseteq A \times A$), we call it a relation on set $A$. Certain properties of relations on a single set are important.
Let $R$ be a relation on a non-empty set $A$, so $R \subseteq A \times A$.
3. Identity Relation: The relation $I_A$ on set $A$ where every element is related only to itself is called the identity relation on $A$.
$I_A = \{ (a, a) : a \in A \}$
For example, if $A = \{1, 2, 3\}$, the identity relation on $A$ is $I_A = \{(1, 1), (2, 2), (3, 3)\}$.
4. Reflexive Relation: A relation $R$ on set $A$ is said to be reflexive if every element in $A$ is related to itself. This means that for every element $a$ in set $A$, the ordered pair $(a, a)$ must be present in the relation $R$.
$R \text{ is reflexive } \iff \forall a \in A, (a, a) \in R$
5. Symmetric Relation: A relation $R$ on set $A$ is said to be symmetric if whenever an element $a$ is related to an element $b$, then $b$ is also related to $a$. This means that for all $a, b \in A$, if the ordered pair $(a, b)$ is in $R$, then the ordered pair $(b, a)$ must also be in $R$.
$R \text{ is symmetric } \iff \forall a, b \in A, \text{ if } (a, b) \in R \text{ then } (b, a) \in R$
6. Transitive Relation: A relation $R$ on set $A$ is said to be transitive if whenever $a$ is related to $b$ and $b$ is related to $c$, then $a$ is also related to $c$. This means that for all $a, b, c \in A$, if the ordered pair $(a, b)$ is in $R$ and the ordered pair $(b, c)$ is in $R$, then the ordered pair $(a, c)$ must also be in $R$.
$R \text{ is transitive } \iff \forall a, b, c \in A, \text{ if } (a, b) \in R \text{ and } (b, c) \in R \text{ then } (a, c) \in R$
7. Equivalence Relation: A relation $R$ on a set $A$ is called an equivalence relation if it satisfies all three properties: it is reflexive, symmetric, and transitive.
Equivalence relations partition a set into disjoint equivalence classes, where all elements within a class are related to each other.
Example 2. Let $A = \{1, 2, 3\}$. Examine if the relation $R = \{ (1, 1), (2, 2), (3, 3), (1, 2), (2, 3) \}$ on $A$ is reflexive, symmetric, or transitive.
Answer:
Given:
Set $A = \{1, 2, 3\}$
Relation $R = \{ (1, 1), (2, 2), (3, 3), (1, 2), (2, 3) \}$ on $A$.
To Examine:
Whether $R$ is reflexive, symmetric, or transitive.
Solution:
We will examine each property one by one.
1. Check for Reflexivity
Condition: A relation is reflexive if for every element $a \in A$, the ordered pair $(a, a)$ is in $R$.
The elements in our set $A$ are 1, 2, and 3. So, for $R$ to be reflexive, it must contain the pairs $(1, 1)$, $(2, 2)$, and $(3, 3)$.
Let's check our given relation $R = \{ (1, 1), (2, 2), (3, 3), (1, 2), (2, 3) \}$.
- Is $(1, 1) \in R$? Yes.
- Is $(2, 2) \in R$? Yes.
- Is $(3, 3) \in R$? Yes.
Since the condition $(a, a) \in R$ is met for every element in $A$, the relation $R$ is reflexive.
2. Check for Symmetry
Condition: A relation is symmetric if whenever an ordered pair $(a, b)$ is in $R$, its "mirror image" pair $(b, a)$ must also be in $R$. If we find even one pair $(a, b)$ in $R$ whose mirror image $(b, a)$ is not in $R$, the relation is not symmetric.
Let's examine the non-reflexive pairs in $R$: $(1, 2)$ and $(2, 3)$.
- Consider the pair $(1, 2) \in R$. For symmetry, its mirror image $(2, 1)$ must also be in $R$.
Looking at $R = \{ (1, 1), (2, 2), (3, 3), (1, 2), (2, 3) \}$, we find that the pair $(2, 1)$ is not present.
Since we have found a counter-example ($(1, 2) \in R$ but $(2, 1) \notin R$), we can immediately conclude that the relation $R$ is not symmetric. (We don't even need to check the pair $(2, 3)$).
3. Check for Transitivity
Condition: A relation is transitive if whenever there is a "chain" of pairs $(a, b) \in R$ and $(b, c) \in R$, there must exist a "direct link" pair $(a, c) \in R$. If we find a single broken chain, the relation is not transitive.
We need to look for all instances of $(a,b)$ and $(b,c)$ in $R$ and check if $(a,c)$ is also present.
Let's systematically search for such chains in $R = \{ (1, 1), (2, 2), (3, 3), (1, 2), (2, 3) \}$.
- We see a pair $(1, 2)$ which ends with 2.
- We see a pair $(2, 3)$ which starts with 2.
This forms a chain: $(1, 2) \in R$ and $(2, 3) \in R$. Here, $a=1, b=2,$ and $c=3$.
For transitivity, the direct link $(a, c) = (1, 3)$ must be in $R$.
Let's check our relation $R$. Is the pair $(1, 3)$ present? No, it is not.
Since we found a chain $(1, 2)$ and $(2, 3)$ for which the direct link $(1, 3)$ is missing, the relation $R$ is not transitive.
Conclusion
Based on our examination of the three properties:
- The relation is Reflexive.
- The relation is Not Symmetric.
- The relation is Not Transitive.
Representation of a Relation
A relation from one set to another is fundamentally a set of ordered pairs. While simply listing these ordered pairs (Roster Form) is one way to represent a relation, there are other methods that can be more convenient or insightful depending on the nature of the relation or the context of the problem. Here are some common ways to represent a relation $R$ from set $A$ to set $B$ ($R \subseteq A \times B$):
1. Roster Form (Set of Ordered Pairs):
As per the definition, a relation $R$ from $A$ to $B$ is a subset of $A \times B$. The most direct way to specify such a subset is by listing all the ordered pairs $(a, b)$ that are included in the relation. This is known as the Roster Form or listing method.
Example:
Let $A = \{1, 2\}$ and $B = \{x, y\}$. The Cartesian product is $A \times B = \{ (1, x), (1, y), (2, x), (2, y) \}$.
Consider a relation $R$ from $A$ to $B$ where $1$ is related to $x$ and $y$, and $2$ is related to $x$. In Roster Form, this relation is explicitly written as the set of these ordered pairs:
$R = \{ (1, x), (1, y), (2, x) \}$
...(1)
This form is clear and complete, especially for relations with a small number of ordered pairs.
2. Set-Builder Form:
For relations defined by a specific property or rule that connects the elements of the ordered pairs, the Set-Builder Form is a concise way to represent the relation. It describes the relation by stating the property that the elements of the ordered pairs must satisfy to be included in the relation.
A relation $R$ from $A$ to $B$ in Set-Builder Form is written as:
$R = \{ (a, b) \in A \times B : P(a, b) \text{ is true} \}$
... (2)
Here, $P(a, b)$ represents the property or condition that relates element $a$ from set $A$ to element $b$ from set $B$. The notation $(a, b) \in A \times B$ specifies that we are considering ordered pairs formed by elements from $A$ and $B$.
Example:
Let $A = \{1, 2, 3, 4, 5\}$ and $B = \{1, 2, 3, 4, 5, 6\}$. Consider the relation $R$ from $A$ to $B$ defined by the rule "$a$ is one less than $b$". In Set-Builder Form, this relation is written as:
$R = \{ (a, b) \in A \times B : a = b - 1 \}$
To verify this, let's find the ordered pairs $(a, b)$ from $A \times B$ that satisfy $a = b - 1$ (or $b = a + 1$):
If $a=1$, $b = 1+1 = 2$. Since $1 \in A$ and $2 \in B$, $(1, 2)$ is in $R$.
If $a=2$, $b = 2+1 = 3$. Since $2 \in A$ and $3 \in B$, $(2, 3)$ is in $R$.
If $a=3$, $b = 3+1 = 4$. Since $3 \in A$ and $4 \in B$, $(3, 4)$ is in $R$.
If $a=4$, $b = 4+1 = 5$. Since $4 \in A$ and $5 \in B$, $(4, 5)$ is in $R$.
If $a=5$, $b = 5+1 = 6$. Since $5 \in A$ and $6 \in B$, $(5, 6)$ is in $R$.
If we take $a=6$, $b = 6+1 = 7$. But $6 \notin A$, so we stop at $a=5$.
If we take $b=1$, $a = 1-1 = 0$. But $0 \notin A$.
If we take $b=7$, $a = 7-1 = 6$. But $6 \notin A$.
So, in Roster Form, this relation is $R = \{ (1, 2), (2, 3), (3, 4), (4, 5), (5, 6) \}$. Both forms represent the same relation.
3. Arrow Diagram (Mapping Diagram):
An Arrow Diagram provides a visual representation of a relation, particularly useful for finite sets. It is also sometimes called a Mapping Diagram.
To create an arrow diagram for a relation $R$ from set $A$ to set $B$:
- Draw two closed shapes (usually ovals or rectangles), one representing set $A$ and the other representing set $B$.
- List the elements of set $A$ inside the shape for $A$, and the elements of set $B$ inside the shape for $B$.
- For every ordered pair $(a, b)$ that belongs to the relation $R$ (where $a \in A$ and $b \in B$), draw an arrow starting from the element $a$ in set $A$ and pointing to the element $b$ in set $B$.
Example:
Let $A = \{1, 2, 3\}$ and $B = \{x, y\}$. Let the relation $R$ from $A$ to $B$ be given in Roster Form as $R = \{ (1, x), (1, y), (2, x) \}$.
To draw the arrow diagram, we show the elements and draw arrows corresponding to the ordered pairs in $R$:
- Draw an arrow from 1 to x (since $(1, x) \in R$).
- Draw an arrow from 1 to y (since $(1, y) \in R$).
- Draw an arrow from 2 to x (since $(2, x) \in R$).
- There is no arrow from 3 to any element in B (since no pair $(3, b)$ is in $R$).
- There is no arrow from 2 to y (since $(2, y) \notin R$).
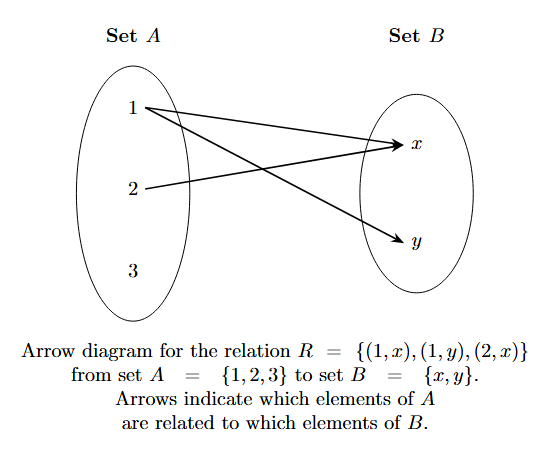
This diagram visually represents the relation $R = \{ (1, x), (1, y), (2, x) \}$. It clearly shows which elements are related.
4. Matrix Representation:
For finite sets, a relation can also be represented using a matrix. This method is particularly useful in discrete mathematics and computer science.
Let $A = \{a_1, a_2, ..., a_p\}$ be a finite set with $p$ elements, and $B = \{b_1, b_2, ..., b_q\}$ be a finite set with $q$ elements. A relation $R$ from $A$ to $B$ can be represented by a $p \times q$ matrix $M_R$, called the relation matrix.
The entries of the matrix are defined as follows:
$m_{ij} = \begin{cases} 1 & \text{if } (a_i, b_j) \in R \\ 0 & \text{if } (a_i, b_j) \notin R \end{cases}$
The rows of the matrix correspond to the elements of set $A$, and the columns correspond to the elements of set $B$. The entry in the $i$-th row and $j$-th column is 1 if the $i$-th element of $A$ is related to the $j$-th element of $B$, and 0 otherwise.
Example:
Let $A = \{1, 2\}$ and $B = \{x, y, z\}$. Let the relation $R$ from $A$ to $B$ be $R = \{ (1, x), (1, z), (2, y) \}$.
Set $A$ has elements $a_1=1, a_2=2$. Set $B$ has elements $b_1=x, b_2=y, b_3=z$. The relation matrix will be a $2 \times 3$ matrix $M_R = \begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \end{bmatrix}$.
- $m_{11}$: Is $(a_1, b_1) = (1, x)$ in $R$? Yes. So, $m_{11} = 1$.
- $m_{12}$: Is $(a_1, b_2) = (1, y)$ in $R$? No. So, $m_{12} = 0$.
- $m_{13}$: Is $(a_1, b_3) = (1, z)$ in $R$? Yes. So, $m_{13} = 1$.
- $m_{21}$: Is $(a_2, b_1) = (2, x)$ in $R$? No. So, $m_{21} = 0$.
- $m_{22}$: Is $(a_2, b_2) = (2, y)$ in $R$? Yes. So, $m_{22} = 1$.
- $m_{23}$: Is $(a_2, b_3) = (2, z)$ in $R$? No. So, $m_{23} = 0$.
The relation matrix $M_R$ is:
| x | y | z | |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | 0 | 1 | 0 |
This matrix conveniently summarizes which pairs of elements from $A$ and $B$ are related according to $R$.
These different representations offer various ways to view and work with relations, each having its advantages depending on the specific application.
Domain, Codomain, and Range of a Relation
For any relation from a set $A$ to a set $B$, we use specific terms to describe the collection of elements involved. The concepts of domain, codomain, and range help us understand the scope and the actual output of the relation.
An arrow diagram is an excellent way to visualize these concepts.
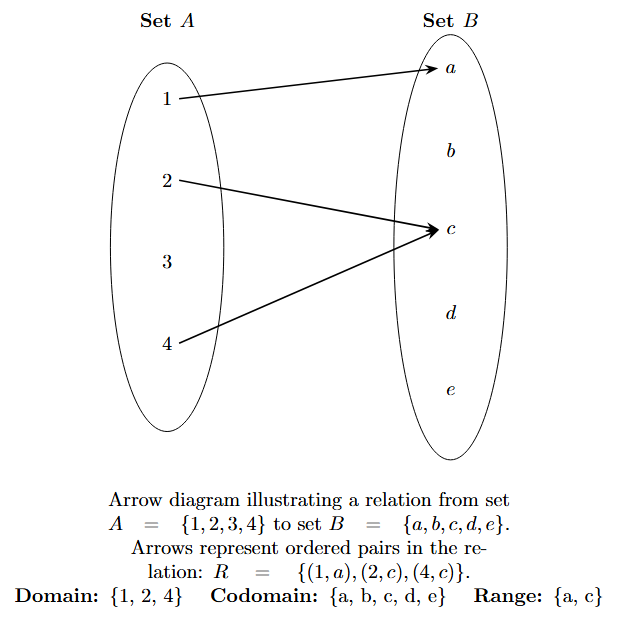
Based on the diagram above:
- The Domain is the set of all starting points of the arrows: $\{1, 2, 4\}$.
- The Codomain is the entire set of all possible destinations: $\{a, b, c, d, e\}$.
- The Range is the set of all actual destinations where the arrows land: $\{a, c\}$.
Domain of a Relation
The domain of a relation $R$ from set $A$ to set $B$ is the set of all first elements from the ordered pairs in $R$. It represents all the elements in the starting set $A$ that are actually used in the relation.
Symbolic Definition:
The domain of $R$ is defined as:
Domain($R$) $= \{ a : (a, b) \in R \text{ for some } b \in B \}$
Essentially, Domain($R$) $\subseteq A$.
Codomain of a Relation
When a relation $R$ is defined from a set $A$ to a set $B$, the entire destination set $B$ is called the codomain of the relation. It represents the set of all possible second elements.
Codomain($R$) $= B$
Range of a Relation
The range of a relation $R$ is the set of all second elements from the ordered pairs in $R$. It represents the set of elements in the codomain that are actually reached or mapped to by the relation.
Symbolic Definition:
The range of $R$ is defined as:
Range($R$) $= \{ b : (a, b) \in R \text{ for some } a \in A \}$
By definition, the range is always a subset of the codomain: Range($R$) $\subseteq$ Codomain($R$).
Example 1. Let $A = \{1, 2, 3, 4, 5, 6\}$. Define a relation $R$ from $A$ to $A$ by $R = \{ (x, y) : y = x + 1 \}$. Write down the Domain, Codomain, and Range of $R$.
Answer:
Given:
The set is $A = \{1, 2, 3, 4, 5, 6\}$.
The relation is $R$ from $A$ to $A$, defined by the rule $y = x + 1$.
Solution:
Step 1: Determine the ordered pairs in the relation.
We need to find all pairs $(x, y)$ where $x \in A$, $y \in A$, and $y = x + 1$. We can do this systematically by taking each value of $x$ from set $A$ and checking if the resulting $y$ is also in set $A$.
| Value of $x$ (from A) | Calculate $y = x+1$ | Is $y \in A$? | Ordered Pair $(x, y)$ in R? |
|---|---|---|---|
| 1 | $y=1+1=2$ | Yes, $2 \in A$ | Yes, $(1, 2)$ |
| 2 | $y=2+1=3$ | Yes, $3 \in A$ | Yes, $(2, 3)$ |
| 3 | $y=3+1=4$ | Yes, $4 \in A$ | Yes, $(3, 4)$ |
| 4 | $y=4+1=5$ | Yes, $5 \in A$ | Yes, $(4, 5)$ |
| 5 | $y=5+1=6$ | Yes, $6 \in A$ | Yes, $(5, 6)$ |
| 6 | $y=6+1=7$ | No, $7 \notin A$ | No |
So, the relation $R$ in roster form is:
$R = \{ (1, 2), (2, 3), (3, 4), (4, 5), (5, 6) \}$
Step 2: Find the Domain, Codomain, and Range.
Domain(R): This is the set of all the first elements in the pairs of $R$.
First elements are: 1, 2, 3, 4, 5.
$\implies$ Domain($R$) $= \{1, 2, 3, 4, 5\}$
Codomain(R): This is the entire set that the relation maps to. The relation is from $A$ to $A$, so the codomain is $A$.
$\implies$ Codomain($R$) $= \{1, 2, 3, 4, 5, 6\}$
Range(R): This is the set of all the second elements in the pairs of $R$.
Second elements are: 2, 3, 4, 5, 6.
$\implies$ Range($R$) $= \{2, 3, 4, 5, 6\}$
Visual Representation:
The relation can be shown with an arrow diagram as follows:

Functions
A function is a fundamental concept in mathematics that describes a special relationship between two sets. Think of a function as a well-behaved "machine" or a set of rules that takes an input from one set and produces exactly one output in another set.
Formally, a relation $f$ from a non-empty set $A$ to a non-empty set $B$ is called a function if every element of set $A$ is associated with one and only one element in set $B$.
We denote a function $f$ from set $A$ to set $B$ as $f: A \to B$.
- Set $A$ is called the Domain of the function (the set of all possible inputs).
- Set $B$ is called the Codomain of the function (the set of all possible outputs).
If an element $a \in A$ is mapped to an element $b \in B$ by the function $f$, we write $f(a) = b$. Here, $b$ is the image of $a$, and $a$ is the preimage of $b$.
The Two Golden Rules of Functions
For a relation from a set $A$ to a set $B$ to be a function, it must obey two strict rules:
1. Every Input Must Have an Output: Every element in the domain (set $A$) must be used as an input. No element in $A$ can be left out or ignored.
2. Each Input Must Have Exactly One Output: An input from set $A$ cannot be mapped to two or more different outputs in set $B$. The output must be unique for each input.
Visualizing the Rules with Arrow Diagrams
Let's use arrow diagrams to see which relations are functions and which are not. Let $A = \{1, 2, 3\}$ and $B = \{a, b, c\}$.
This IS a function:

It obeys both rules. Every element in A has one, and only one, outgoing arrow.
This is NOT a function: (Violates Rule 1)

The input '3' from set A has no output. It is left out.
This is NOT a function: (Violates Rule 2)

The input '1' has two different outputs, 'a' and 'b'.
This IS a function: (Many-to-One)

This is perfectly fine! It is okay for multiple inputs to have the same output. Rule 2 is not violated because each input still has only one outgoing arrow.
The Vertical Line Test
For graphs on a coordinate plane, the Vertical Line Test is a simple visual method to check if a graph represents a function.
Rule: If you can draw any vertical line that intersects the graph at more than one point, the graph does NOT represent a function. If all possible vertical lines intersect the graph at most once, it IS a function.
A vertical line represents a single input value (an x-value). If it hits the graph twice, it means that one input has two different outputs (y-values), which violates Rule 2.
IS a Function (e.g., $y=x^2$)

Any vertical line will cross the graph only once.
NOT a Function (e.g., a circle)
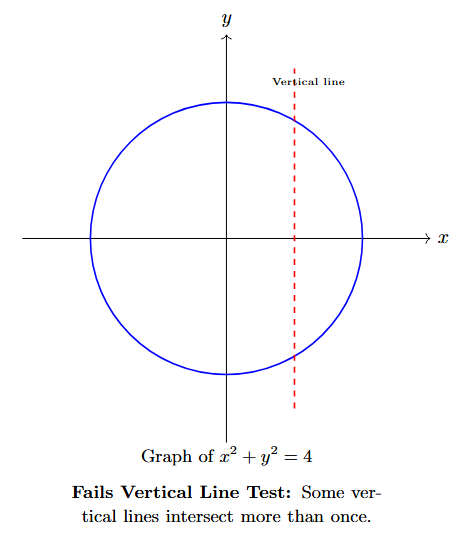
A vertical line can cross the graph in two places.
Domain, Codomain, and Range of a Function
These terms, previously defined for relations, have a more specific meaning for functions due to the strict rules a function must follow.
Let's consider a function $f: A \to B$. The notation itself provides key information.
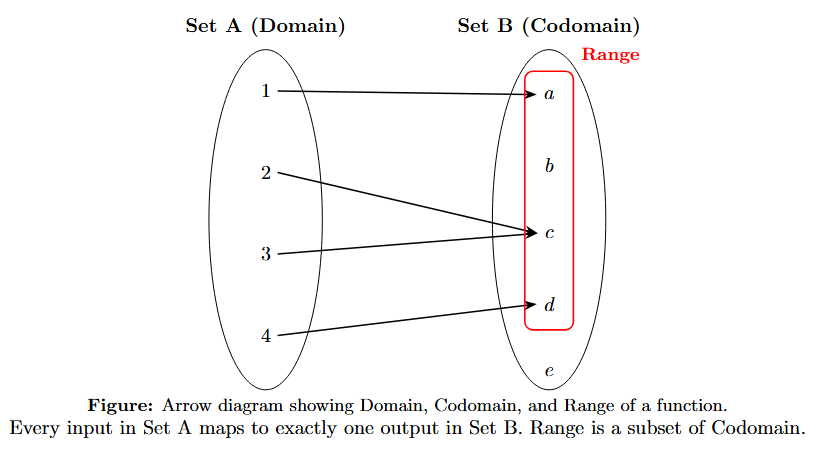
Domain of a Function
The domain is the set of all valid inputs for the function. For a function defined as $f: A \to B$, the domain is the entire starting set $A$. This is a direct consequence of Rule 1 of functions (every input must have an output).
Domain($f$) $= A$
Codomain of a Function
The codomain is the set of all possible outputs. For a function defined as $f: A \to B$, the codomain is the entire destination set $B$. It's the "universe" of values that the output of the function is allowed to be in.
Codomain($f$) $= B$
Range of a Function
The range is the set of all actual outputs the function produces when you plug in every element from the domain. The range is the set of all images of the elements of the domain.
The range is always a subset of the codomain. It can be equal to the codomain, or it can be smaller.
Range($f$) $= \{ f(a) : a \in A \}$
This means the range is the set you get by applying the function to every single element in the domain. Therefore, Range($f$) $\subseteq$ Codomain($f$).
Example 1. A function $f$ is defined from the set of integers $\mathbb{Z}$ to itself ($\mathbb{Z}$) by the rule $f(x) = x^2$. Find the domain, codomain, and range of $f$.
Answer:
Given:
The function is defined as $f: \mathbb{Z} \to \mathbb{Z}$, where $\mathbb{Z} = \{\dots, -2, -1, 0, 1, 2, \dots\}$.
The function rule is $f(x) = x^2$.
Solution:
1. Domain:
The domain is the set of all allowed inputs. Since the function is defined as $f: \mathbb{Z} \to \mathbb{Z}$, the starting set (the domain) is the set of all integers, $\mathbb{Z}$.
Domain($f$) $= \mathbb{Z}$
2. Codomain:
The codomain is the set of all possible outputs. Since the function is defined as $f: \mathbb{Z} \to \mathbb{Z}$, the destination set (the codomain) is also the set of all integers, $\mathbb{Z}$.
Codomain($f$) $= \mathbb{Z}$
3. Range:
The range is the set of all actual outputs we get by applying the rule $f(x) = x^2$ to every integer in the domain.
Let's test some inputs:
- $f(0) = 0^2 = 0$
- $f(1) = 1^2 = 1$
- $f(-1) = (-1)^2 = 1$
- $f(2) = 2^2 = 4$
- $f(-2) = (-2)^2 = 4$
- $f(3) = 3^2 = 9$
- $f(-3) = (-3)^2 = 9$
We can observe a pattern: the output of $f(x) = x^2$ is always a non-negative integer. Specifically, the outputs are the perfect squares: 0, 1, 4, 9, 16, 25, and so on. It is impossible to get a negative number or an integer that is not a perfect square (like 2, 3, 5, etc.) as an output.
Therefore, the set of actual outputs is the set of all non-negative perfect squares.
Range($f$) $= \{0, 1, 4, 9, 16, 25, \dots\} \ $$ = \{k^2 : k \ $$ \text{ is a} \ $$ \text{non-negative} \ $$ \text{ integer}\}$
Notice that the Range $\{0, 1, 4, \dots\}$ is a proper subset of the Codomain $\mathbb{Z}$.
Main Features of a Function
A function, denoted as $f: A \to B$, is more than just a set of ordered pairs; it is a structured mathematical concept with several defining characteristics. Understanding these features helps to clarify why functions are so essential in mathematics.
1. A Function is a Definitive Rule
At its core, a function is a rule of assignment or a mapping. It provides a precise instruction for taking any element from the domain (set $A$) and associating it with a specific element in the codomain (set $B$).
Analogy: Think of a function as a recipe. The domain is your set of possible ingredients (inputs), and the codomain is the set of all possible dishes you could make (outputs). The function itself is the set of instructions in the recipe that turns a specific ingredient into a specific dish.
2. The Two Non-Negotiable Rules
For any relation to qualify as a function, it must strictly adhere to two conditions:
(a) Every Element in the Domain Must Be Mapped: The function must be defined for every single element in its domain. No element in set $A$ can be "left out" or have no corresponding image in set $B$. This is why for a function $f: A \to B$, we say Domain($f$) = $A$.
(b) The Image Must Be Unique: Each element in the domain can be mapped to one and only one element in the codomain. An input cannot produce two or more different outputs. This guarantees that a function's output is predictable and unambiguous.
3. The Concept of Preimages (Working Backwards)
While every input (domain element) has exactly one output (image), the reverse is not necessarily true. An element in the codomain can be the image of zero, one, or multiple elements from the domain. The set of inputs that map to a specific output is called its preimage.
The preimage of an element $b \in B$ is the set of all $a \in A$ such that $f(a) = b$.
Preimage($b$) $= \{ a \in A : f(a) = b \}$
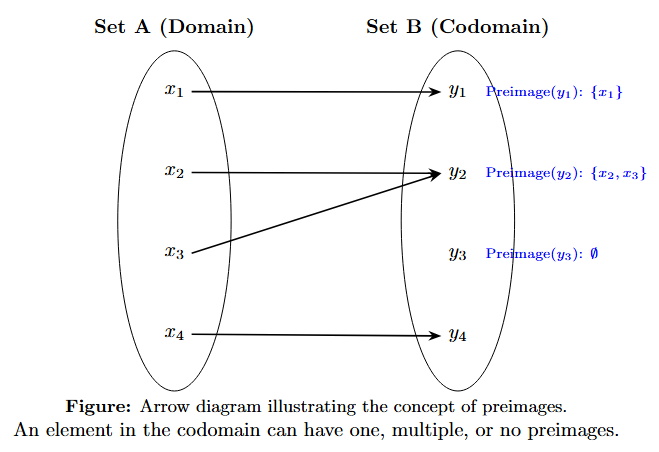
4. Range vs. Codomain: Actual vs. Possible
It's crucial to distinguish between the codomain and the range.
- The Codomain is the entire set $B$ of all possible outputs. It is declared as part of the function's definition ($f: A \to B$).
- The Range is the set of all actual outputs that the function generates. It is the collection of all images and is always a subset of the codomain.
Analogy: Imagine a vending machine. The codomain is every single item listed on the buttons (Coke, Pepsi, Sprite, Water, Chips, etc.). The range is only the items that are actually in stock. If the machine is out of Sprite, then Sprite is in the codomain but not in the range.
Range($f$) $\subseteq$ Codomain($f$)
5. Equality of Functions
Two functions, $f$ and $g$, are considered equal if and only if they are identical in every aspect. This requires three conditions to be met simultaneously:
- Same Domain: Domain($f$) must be equal to Domain($g$).
- Same Codomain: Codomain($f$) must be equal to Codomain($g$).
- Same Rule of Assignment: For every element $x$ in their shared domain, the output must be the same: $f(x) = g(x)$.
For example, let $f: \mathbb{R} \to \mathbb{R}$ be defined by $f(x) = x^2$ and $g: \mathbb{N} \to \mathbb{R}$ be defined by $g(x) = x^2$. Even though they have the same formula, $f$ and $g$ are not equal functions because their domains are different.
Example: A Detailed Look
Let's illustrate these features with an example.
Let $f: \mathbb{Z} \to \mathbb{Z}$ be a function defined by the rule $f(x) = x - 5$, where $\mathbb{Z}$ is the set of all integers.
Domain and Codomain
From the definition $f: \mathbb{Z} \to \mathbb{Z}$, we can immediately identify:
- Domain: The set of all integers, $\mathbb{Z}$.
- Codomain: The set of all integers, $\mathbb{Z}$.
Range
The range is the set of all actual outputs $\{f(x) : x \in \mathbb{Z}\}$. Let's see what outputs we get:
...
$f(-2) = -2 - 5 = -7$
$f(-1) = -1 - 5 = -6$
$f(0) = 0 - 5 = -5$
$f(1) = 1 - 5 = -4$
$f(2) = 2 - 5 = -3$
...
Since for any integer $y$ we can find an integer input $x=y+5$ that produces it, every integer in the codomain can be an output. Thus, the range is the entire set of integers.
Range($f$) $= \mathbb{Z}$. In this case, Range($f$) = Codomain($f$).
Image and Preimage
- Image of an element: To find the image of, say, 10, we apply the function rule:
$f(10) = 10 - 5 = 5$. The image of 10 is 5.
- Preimage of an element: To find the preimage of, say, 10, we look for all inputs $x$ that produce an output of 10.
Set $f(x) = 10 \implies x - 5 = 10 \implies x = 15$.
Since $15 \in \mathbb{Z}$ (our domain), the only input that gives 10 is 15.Preimage(10) = $\{15\}$.
Real Functions
In mathematics, the concept of a function can be applied to any type of set. However, in algebra, trigonometry, and calculus, our primary focus is on functions where the inputs and outputs are real numbers. These are known as real functions.
A function $f: A \to B$ is called a real function if its domain $A$ is a subset of the real numbers ($\mathbb{R}$) and its codomain $B$ is also a subset of the real numbers ($\mathbb{R}$).
In simpler terms, a real function is a rule that takes a real number as an input and produces a real number as an output.
To be more precise, we can break this definition into two parts:
Real-Valued Function (Output is Real)
A function is real-valued if its codomain is a subset of $\mathbb{R}$. This means its output values are real numbers, but its input can be anything.
Example: Consider a function that takes a person's name as input and gives their height in centimeters as output.
$f(\text{'Alice'}) = 165$
$f(\text{'Bob'}) = 178$
The domain is a set of names (not real numbers), but the codomain is a set of heights (real numbers). This is a real-valued function.
Function of a Real Variable (Input is Real)
A function is a function of a real variable if its domain is a subset of $\mathbb{R}$. This means its input must be a real number, but its output can be anything.
Example: Consider a function that takes time (in seconds) as input and gives your GPS coordinates (an ordered pair) as output.
$g(t) = (\text{latitude}, \text{longitude})$
$g(10) = (28.61^\circ N, 77.23^\circ E)$
The domain is a set of real numbers (time), but the codomain is a set of ordered pairs (not real numbers). This is a function of a real variable.
A real function is the intersection of these two ideas: it is both real-valued and a function of a real variable.
| Type of Function | Input (Domain) $\subseteq \mathbb{R}$? | Output (Codomain) $\subseteq \mathbb{R}$? | Description |
|---|---|---|---|
| Real-Valued | Not necessarily | Yes | The output is a real number. |
| Of a Real Variable | Yes | Not necessarily | The input is a real number. |
| Real Function | Yes | Yes | Both input and output are real numbers. |
Most functions you are familiar with, like $f(x) = 2x+1$, $g(x) = \sin(x)$, and $h(x) = \sqrt{x}$, are real functions because they take a real number $x$ and produce a real number $f(x)$. From here on, when we refer to a "function", we will typically mean a real function.
Domain and Range of a Real Function
For real functions defined by a formula (e.g., $f(x) = \sqrt{x-2}$), the domain and range aren't always explicitly stated. We often need to determine them by analyzing the formula and identifying which real numbers are valid inputs and which real numbers can be generated as outputs.
How to Determine the Domain of a Real Function
The domain of a function is the complete set of all possible input values (x-values) for which the function's formula is defined and produces a valid, real number output. When given a function's formula, a practical approach is to assume the domain is all real numbers ($\mathbb{R}$) and then systematically identify and exclude any values that would violate fundamental mathematical principles.
Identifying Potential Domain Restrictions
We look for mathematical operations that are not defined for all real numbers. The most common restrictions arise from the following situations:
1. Fractions (Avoiding Division by Zero)
- The Principle: Division by zero is mathematically undefined.
- The Condition: In any fractional expression of the form $f(x) = \frac{P(x)}{Q(x)}$, the denominator $Q(x)$ cannot be equal to zero.
- How to Apply: Set the expression in the denominator to be not equal to zero ($Q(x) \neq 0$) and solve for $x$. The values of $x$ you find are the ones that must be excluded from the domain.
- Example: For the function $f(x) = \frac{x+1}{x-3}$, we must enforce the condition $x-3 \neq 0$. Solving this gives $x \neq 3$. Therefore, the domain is the set of all real numbers except 3, which can be written as $\mathbb{R} - \{3\}$ or in interval notation as $(-\infty, 3) \cup (3, \infty)$.
2. Even-Indexed Roots (like Square Roots)
- The Principle: Within the set of real numbers, it is not possible to take an even-indexed root (square root, fourth root, etc.) of a negative number.
- The Condition: For an expression of the form $f(x) = \sqrt[n]{g(x)}$ where $n$ is an even integer, the expression inside the root (the radicand), $g(x)$, must be non-negative.
- How to Apply: Set the expression inside the root to be greater than or equal to zero ($g(x) \ge 0$) and solve the resulting inequality.
- Example: For the function $g(x) = \sqrt{x-4}$, we must enforce the condition $x-4 \ge 0$. Solving this gives $x \ge 4$. Therefore, the domain is the set of all real numbers greater than or equal to 4, written as $[4, \infty)$.
3. Logarithms
- The Principle: The logarithm of a number is only defined for strictly positive numbers.
- The Condition: For an expression of the form $f(x) = \log_b(g(x))$, the argument of the logarithm, $g(x)$, must be strictly positive.
- How to Apply: Set the argument of the logarithm to be greater than zero ($g(x) > 0$) and solve the resulting inequality.
- Example: For the function $h(x) = \log(x+2)$, we must enforce the condition $x+2 > 0$. Solving this gives $x > -2$. Therefore, the domain is the set of all real numbers greater than -2, written as $(-2, \infty)$.
Combining Multiple Restrictions
If a function involves more than one of these restrictions, its domain must satisfy all conditions simultaneously. To find the overall domain, you find the domain for each individual restriction and then determine the intersection of those sets.
Example: For $f(x) = \frac{1}{\sqrt{x-5}}$:
- From the square root: The expression inside, $x-5$, must be non-negative. So, $x-5 \ge 0 \implies x \ge 5$.
- From the fraction: The denominator, $\sqrt{x-5}$, cannot be zero. So, $\sqrt{x-5} \neq 0 \implies x-5 \neq 0 \implies x \neq 5$.
We must satisfy both conditions: $x \ge 5$ AND $x \neq 5$. The only way to satisfy both is for $x$ to be strictly greater than 5. Thus, the domain is $(5, \infty)$.
How to Determine the Range of a Real Function
The range of a function is the complete set of all possible output values (y-values) it can produce, given its domain. Determining the range can often be more intricate than finding the domain because it requires understanding the function's behavior and the set of values it can generate. Here are the primary methods for finding the range.
Method 1: Analytical Method (Reasoning about the Function's Properties)
This method involves a logical analysis of the function's formula, especially for functions whose structure inherently limits their output values. It is often the quickest method if the function is simple.
Look for these common structures:
- Even Powers (e.g., $x^2, x^4, \dots$): Any real number raised to an even power results in a non-negative number. For example, $x^2 \ge 0$.
- Even Roots (e.g., $\sqrt{x}, \sqrt[4]{x}, \dots$): The principal even root of a number is, by definition, always non-negative. For example, $\sqrt{g(x)} \ge 0$.
- Absolute Value (e.g., $|x|$): The absolute value of any real number is always non-negative. For example, $|g(x)| \ge 0$.
- Certain Trigonometric Functions: Functions like $\sin(x)$ and $\cos(x)$ have a bounded output, oscillating between -1 and 1. Their range is $[-1, 1]$.
Example: Find the range of $f(x) = x^2 + 5$.
- Start with the core component: We know that for any real number $x$, $x^2 \ge 0$.
- Build the function: To get our function $f(x)$, we need to add 5. We can add 5 to both sides of the inequality:
$x^2 + 5 \ge 0 + 5$
$x^2 + 5 \ge 5$
- Conclude the range: Since $f(x) = x^2 + 5$, this means $f(x) \ge 5$. The function can produce any value greater than or equal to 5. The range is $[5, \infty)$.
Method 2: Algebraic Method (Expressing x in terms of y)
This is a powerful and systematic technique that works for many algebraic functions, especially rational functions. The core idea is to treat the output $y$ as a known value and see what constraints that places on the input $x$.
The process is as follows:
- Replace $f(x)$ with $y$, so you have the equation $y = f(x)$.
- Rearrange the equation to solve for $x$ in terms of $y$.
- Analyze the resulting expression for $x$. The set of all possible real values for $y$ for which the expression for $x$ is defined constitutes the range of the original function $f(x)$. (Essentially, you are finding the "domain" of the inverse relation).
Example: Find the range of $f(x) = \frac{x+1}{x-3}$.
- Let $y = \frac{x+1}{x-3}$.
- Solve for $x$:
$y(x-3) = x+1$
$xy - 3y = x+1$
$xy - x = 3y+1$
$x(y - 1) = 3y+1$
$x = \frac{3y+1}{y-1}$
- Analyze the expression for $x$. For $x$ to be a real number, the denominator of this new expression cannot be zero. Therefore, $y-1 \neq 0$, which means $y \neq 1$. This implies that the original function can produce any real number output except for 1. The range is $\mathbb{R} - \{1\}$.
Method 3: Graphical Method (Visual Inspection)
If you know the shape of the function's graph or can sketch it accurately, you can determine the range visually. The range is the set of all y-values that the graph covers.
The process is as follows:
- Sketch the graph of the function $y = f(x)$.
- Imagine projecting the entire graph horizontally onto the y-axis.
- The portion of the y-axis that this "shadow" covers is the range of the function.
Example: Find the range of $f(x) = \sqrt{x-4}$.
We will find the range of the function by first determining the domain (the set of possible input values) and then analyzing the function's output based on that domain, which can be visualized with a graph.
Step 1: Determine the Domain
The function $f(x) = \sqrt{x-4}$ involves a square root. For the output to be a real number, the expression inside the square root must be non-negative.
Therefore, we must have:
$x - 4 \geq 0$
$x \geq 4$
So, the domain of the function is all real numbers greater than or equal to 4, which is written in interval notation as $[4, \infty)$. This means the graph of the function will start at $x=4$ and extend infinitely to the right.
Step 2: Analyze the Graph and Find the Range
The process to find the range from the graph is as follows:
- Sketch the graph: We know this is the graph of the basic square root function, $y=\sqrt{x}$, shifted 4 units to the right. The graph starts at the point corresponding to the minimum value in the domain, which is $x=4$.
At $x=4$, the function value is $f(4) = \sqrt{4-4} = 0$.
So, the starting point of the graph is $(4, 0)$. As $x$ increases, the value of $\sqrt{x-4}$ also increases, causing the graph to curve upwards and to the right.
Let's find some coordinates to help visualize the graph. To get integer outputs, we choose x-values such that $(x-4)$ is a perfect square.
$x$ $f(x) = \sqrt{x-4}$ 4 $\sqrt{4-4} = 0$ 5 $\sqrt{5-4} = 1$ 8 $\sqrt{8-4} = 2$ 13 $\sqrt{13-4} = 3$ 20 $\sqrt{20-4} = 4$ - Project onto the y-axis: To determine the range, we observe all the possible y-values covered by the graph.
- The lowest point on the graph is $(4, 0)$, so the minimum y-value is 0.
- As $x$ increases and approaches infinity ($x \to \infty$), the value of $f(x) = \sqrt{x-4}$ also increases without any upper limit ($f(x) \to \infty$).
- Conclude the range: The set of all possible y-values is all real numbers greater than or equal to 0. Therefore, the range of the function is $[0, \infty)$.

Example 1. Find the domain and range of the real function $f(x) = \frac{2x+1}{x-3}$.
Answer:
Finding the Domain:
The function is a fraction. The only restriction is that the denominator cannot be zero.
Set the denominator to not equal zero:
$x - 3 \neq 0$
$x \neq 3$
The domain is all real numbers except for 3.
Domain($f$) $= \mathbb{R} - \{3\}$ or $(-\infty, 3) \cup (3, \infty)$
Finding the Range (using the Algebraic Method):
Step 1: Let $y = f(x)$.
$y = \frac{2x+1}{x-3}$
Step 2: Solve for $x$ in terms of $y$.
$y(x-3) = 2x+1$
(Multiply by $x-3$)
$xy - 3y = 2x+1$
(Distribute $y$)
$xy - 2x = 3y+1$
(Gather $x$ terms on one side)
$x(y - 2) = 3y+1$
(Factor out $x$)
$x = \frac{3y+1}{y-2}$
(Divide by $y-2$)
Step 3: Look for restrictions on $y$.
The expression for $x$ is a fraction. For $x$ to be a real number, the denominator $y-2$ cannot be zero.
$y - 2 \neq 0 \implies y \neq 2$
This means $y$ can be any real number except for 2. This is our range.
Range($f$) $= \mathbb{R} - \{2\}$ or $(-\infty, 2) \cup (2, \infty)$
Example 2. Find the domain and range of the real function $f(x) = \sqrt{9 - x^2}$.
Answer:
Finding the Domain:
The function contains a square root. The expression inside the root must be non-negative.
$9 - x^2 \ge 0$
$9 \ge x^2$
This is equivalent to $x^2 \le 9$. Taking the square root of both sides gives $|x| \le 3$, which means $x$ must be between -3 and 3, inclusive.
$-3 \le x \le 3$
The domain is the closed interval from -3 to 3.
Domain($f$) $= [-3, 3]$
Finding the Range (using Logical Analysis):
Let $y = \sqrt{9 - x^2}$.
1. Minimum Value of y: The square root function, $\sqrt{\cdot}$, by definition, always returns a non-negative value. So, we know $y \ge 0$. The smallest value of $9-x^2$ occurs when $x^2$ is largest. In our domain $[-3, 3]$, the largest value of $x^2$ is $9$ (at $x=3$ or $x=-3$).
When $x = \pm 3$, $y = \sqrt{9 - (\pm 3)^2} = \sqrt{9-9} = \sqrt{0} = 0$.
The minimum value of the range is 0.2. Maximum Value of y: The largest value of $y = \sqrt{9-x^2}$ occurs when the term inside the root, $9-x^2$, is at its maximum. This happens when $x^2$ is as small as possible. In our domain, the smallest value of $x^2$ is $0$ (at $x=0$).
When $x = 0$, $y = \sqrt{9 - 0^2} = \sqrt{9} = 3$.
The maximum value of the range is 3.Combining these, the value of $y$ can be anything from 0 to 3, inclusive.
Range($f$) $= [0, 3]$
Graph of a Real Function
The graph of a real function is a visual representation of the function on the Cartesian plane. It is the collection of all points $(x, y)$ where $x$ is an input from the domain and $y=f(x)$ is the corresponding output.
Essentially, a graph turns the abstract rule of a function into a geometric shape, allowing us to understand its properties intuitively.
Graph of $f = \{ (x, f(x)) : x \in \text{Domain}(f) \}$
Gallery of Common Function Graphs
Recognizing the shapes of basic "parent" functions is a crucial skill. Here are some of the most important ones.
1. Identity Function: $f(x) = x$
A straight line passing through the origin at a 45-degree angle. Each input is equal to its output.
Domain: $\mathbb{R}$
Range: $\mathbb{R}$
2. Constant Function: $f(x) = c$
A horizontal line where the y-value is always $c$, regardless of the x-value.
Domain: $\mathbb{R}$
Range: $\{c\}$
3. Linear Function: $f(x) = mx + c$
A straight line. The value 'm' is the slope (steepness) and 'c' is the y-intercept. It is a generalization of the identity function.
Domain: $\mathbb{R}$
Range: $\mathbb{R}$
4. Modulus (Absolute Value) Function: $f(x) = |x|$
A V-shaped graph with its vertex at the origin. It reflects the negative side of the line $y=x$ across the x-axis.
Domain: $\mathbb{R}$
Range: $[0, \infty)$
5. Quadratic Function (Parabola): $f(x) = x^2$
A U-shaped curve called a parabola, with its vertex at the origin and opening upwards.
Domain: $\mathbb{R}$
Range: $[0, \infty)$
6. Signum Function: $f(x) = \text{sgn}(x)$
A "step" graph that is -1 for negative inputs, 0 for zero, and +1 for positive inputs. Note the open circles indicating points that are not included.
Domain: $\mathbb{R}$
Range: $\{-1, 0, 1\}$
7. Greatest Integer Function: $f(x) = \lfloor x \rfloor$
A step graph that maps a real number to the greatest integer less than or equal to it. Note the closed circle on the left and open circle on the right of each step.
Domain: $\mathbb{R}$
Range: $\mathbb{Z}$ (the set of integers)
8. Least Integer Function (Ceiling Function): $f(x) = \lceil x \rceil$
Also known as the ceiling function, this is a step graph that maps a real number to the least integer greater than or equal to it. Note the open circle on the left and closed circle on the right of each step.
Domain: $\mathbb{R}$
Range: $\mathbb{Z}$ (the set of integers)
9. Fractional Part Function: $f(x) = \{x\} = x - \lfloor x \rfloor$
A sawtooth wave graph that gives the non-negative fractional part of a real number. The value is always between 0 (inclusive) and 1 (exclusive).
Domain: $\mathbb{R}$
Range: $[0, 1)$
10. Rational Function: $f(x) = \frac{1}{x}$
A hyperbola with two branches. The graph approaches the axes but never touches them (asymptotes).
Domain: $\mathbb{R} - \{0\}$
Range: $\mathbb{R} - \{0\}$
11. Exponential Function: $f(x) = a^x, a>1$
A rapidly increasing curve that passes through the point $(0, 1)$. It has a horizontal asymptote at the x-axis ($y=0$).
Domain: $\mathbb{R}$
Range: $(0, \infty)$
12. Logarithmic Function: $f(x) = \log_a(x), a>1$
The inverse of the exponential function. It is a slowly increasing curve passing through $(1, 0)$ with a vertical asymptote at the y-axis ($x=0$).
Domain: $(0, \infty)$
Range: $\mathbb{R}$
What a Graph Tells Us at a Glance
A graph is more than just a picture; it's a rich source of information about a function's behavior.
- Domain and Range:
The domain is the "horizontal spread" of the graph. If you were to squash the graph flat onto the x-axis, the part of the axis it covers is the domain.
The range is the "vertical spread" of the graph. If you were to squash the graph flat onto the y-axis, the part of the axis it covers is the range.
- Zeros of a Function: The points where the graph crosses or touches the x-axis are called the zeros or roots of the function. These are the solutions to the equation $f(x) = 0$.
- Continuity: A function is continuous over an interval if its graph is an unbroken curve. Any jumps, holes, or vertical asymptotes signify a discontinuity.
- One-to-One Property (Horizontal Line Test): A function is one-to-one (meaning each output corresponds to a unique input) if and only if no horizontal line intersects its graph more than once. For example, $f(x)=x^2$ is not one-to-one because a horizontal line like $y=4$ hits the graph at both $x=2$ and $x=-2$.
Some Real Functions
After defining what a real function is and how to find its domain and range in general, let's look at some common and important types of real functions that you will encounter frequently in mathematics. Understanding their definitions, properties, domains, and ranges is crucial for further study.
1. Polynomial Functions
A polynomial function is a real function $f: \mathbb{R} \to \mathbb{R}$ where the output is determined by a polynomial expression in the variable $x$.
The general form of a polynomial function of degree $n$ is:
$f(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0$
Here, $n$ is a non-negative integer representing the degree, and $a_0, a_1, ..., a_n$ are real number coefficients. The leading coefficient, $a_n$, must be non-zero for a polynomial of degree $n>0$.
Common examples include:
- Degree 0: $f(x) = c$ (Constant function)
- Degree 1: $f(x) = ax + b$, where $a \neq 0$ (Linear function)
- Degree 2: $f(x) = ax^2 + bx + c$, where $a \neq 0$ (Quadratic function)
- Degree 3: $f(x) = ax^3 + bx^2 + cx + d$, where $a \neq 0$ (Cubic function)
Domain: A polynomial expression is defined for all real numbers $x$ and always produces a real number output. Therefore, the domain of any polynomial function is the set of all real numbers, $\mathbb{R}$.
Domain of any polynomial function $= \mathbb{R}$
Range: The range of a polynomial function depends on its degree.
For polynomials of odd degree (like linear or cubic functions), the graph extends infinitely in both upward and downward directions. Consequently, the function can take on any real value. The range of an odd-degree polynomial is $\mathbb{R}$.
Range of odd degree polynomial function $= \mathbb{R}$
For polynomials of even degree (like quadratic functions), the graph opens either entirely upwards (if $a_n > 0$) or entirely downwards (if $a_n < 0$). This means the function has a global minimum or a global maximum value, and the range is bounded. For example, the range of $f(x) = x^2$ is $[0, \infty)$, while the range of $f(x) = -x^2+1$ is $(-\infty, 1]$.
Range of even degree polynomial function $\subseteq \mathbb{R}$ (bounded from one side)
2. Rational Functions
A rational function is a function that can be written as the ratio of two polynomial functions, $p(x)$ and $q(x)$.
$f(x) = \frac{p(x)}{q(x)}$, where $p(x)$ and $q(x)$ are polynomials and $q(x)$ is not the zero polynomial.
Domain: A fraction is undefined when its denominator is zero. To find the domain of a rational function, we must identify and exclude all real numbers $x$ that make the denominator $q(x)$ equal to zero.
Domain($f$) $= \{ x \in \mathbb{R} : q(x) \neq 0 \}$
Range: Determining the range of a general rational function can be intricate. It involves analyzing the function's behavior near its asymptotes (vertical, horizontal, or slant) and finding its local maximum or minimum values.
Range of rational function $\subseteq \mathbb{R}$
3. Modulus Function (Absolute Value Function)
The modulus function, or absolute value function, is defined as $f(x) = |x|$. It gives the non-negative distance of a number from zero on the number line.
Its formal definition is piecewise:
$|x| = \begin{cases} x & \text{if } x \ge 0 \\ -x & \text{if } x < 0 \end{cases}$.
Domain: The absolute value is defined for any real number input. Thus, the domain is $\mathbb{R}$.
Domain($f$) $= \mathbb{R}$
Range: The output of the absolute value function is always a non-negative number. The minimum value is 0, and it can take any positive value.
Range($f$) $= [0, \infty)$
4. Signum Function
The signum function, $\text{sgn}(x)$, extracts the sign of a real number. It is defined as:
$f(x) = \text{sgn}(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x = 0 \\ -1 & \text{if } x < 0 \end{cases}$.
Domain: The function provides an output for every possible real number input (positive, negative, or zero). Therefore, its domain is $\mathbb{R}$.
Domain($f$) $= \mathbb{R}$
Range: By its definition, the signum function can only produce three distinct values: -1, 0, or 1.
Range($f$) $= \{-1, 0, 1\}$
5. Greatest Integer Function (Floor Function)
The Greatest Integer Function, or Floor Function, denoted $f(x) = \lfloor x \rfloor$, maps a real number $x$ to the greatest integer that is less than or equal to $x$.
For example: $\lfloor 3.7 \rfloor = 3$, $\lfloor 5 \rfloor = 5$, and $\lfloor -1.2 \rfloor = -2$.
Domain: The floor function is defined for all real numbers. Thus, the domain is $\mathbb{R}$.
Domain($f$) $= \mathbb{R}$
Range: The output of the floor function is, by definition, always an integer. The range is the set of all integers, $\mathbb{Z}$.
Range($f$) $= \mathbb{Z}$
6. Least Integer Function (Ceiling Function)
The Least Integer Function, or Ceiling Function, denoted $f(x) = \lceil x \rceil$, maps a real number $x$ to the least integer that is greater than or equal to $x$.
For example: $\lceil 3.7 \rceil = 4$, $\lceil 5 \rceil = 5$, and $\lceil -1.2 \rceil = -1$.
Domain: The ceiling function is defined for all real numbers. Its domain is $\mathbb{R}$.
Domain($f$) $= \mathbb{R}$
Range: The output of the ceiling function is always an integer. The range is the set of all integers, $\mathbb{Z}$.
Range($f$) $= \mathbb{Z}$
7. Fractional Part Function
The Fractional Part Function, $f(x) = \{x\}$, gives the non-negative fractional part of a number. It is defined as the difference between the number and its floor value.
$\{x\} = x - \lfloor x \rfloor$.
For example: $\{3.7\} = 0.7$, $\{5\} = 0$, and $\{-1.2\} = 0.8$.
Domain: The function is defined for all real numbers, so the domain is $\mathbb{R}$.
Domain($f$) $= \mathbb{R}$
Range: The fractional part of a number is always greater than or equal to 0 and strictly less than 1.
Range($f$) $= [0, 1)$
8. Exponential Function
An exponential function is a function of the form $f(x) = a^x$, where the base $a$ is a positive constant other than 1 ($a > 0, a \neq 1$).
The behavior of the function depends on the base $a$. If $a > 1$, the function shows exponential growth. If $0 < a < 1$, the function shows exponential decay.
Domain: An exponent can be any real number, so the domain is $\mathbb{R}$.
Domain($f$) $= \mathbb{R}$
Range: Since the base $a$ is positive, $a^x$ is always positive. The range is all positive real numbers.
Range($f$) $= (0, \infty)$
9. Logarithmic Function
A logarithmic function, $f(x) = \log_a(x)$, is the inverse of the exponential function. Here, the base $a$ is a positive constant other than 1 ($a > 0, a \neq 1$).
It answers the question: "To what exponent must the base $a$ be raised to get the number $x$?"
Domain: Logarithms are only defined for positive numbers. Therefore, the domain is all positive real numbers.
Domain($f$) $= (0, \infty)$
Range: A logarithm can produce any real number as its output. The range is $\mathbb{R}$.
Range($f$) $= \mathbb{R}$
These fundamental functions can be grouped into broader categories:
Algebraic Functions: These are functions constructed using basic algebraic operations. Polynomials, rational functions, and functions involving roots (e.g., $f(x) = \sqrt{x}$) belong to this group.
Transcendental Functions: These are non-algebraic functions. Exponential and logarithmic functions are key examples, along with trigonometric functions like sin(x) and cos(x).
Piecewise Functions: These functions are defined by different formulas on different parts of their domain. The modulus, signum, floor, ceiling, and fractional part functions are all examples of piecewise-defined functions.
Operations on Real Functions
Just as we can perform algebraic operations like addition, subtraction, multiplication, and division on real numbers, we can also define these operations for real functions. By combining two functions, we create a new function.
This section explains how these operations are defined and, crucially, how to determine the domain of the newly created function. Let's consider two real functions, $f$ and $g$, with their respective domains, Domain($f$) and Domain($g$).
The Common Domain: A Crucial First Step
For any operation that combines $f(x)$ and $g(x)$, the new function can only be defined for an input $x$ where both original functions are defined. If an $x$ value is in the domain of $f$ but not $g$ (or vice versa), we cannot perform the operation.
This means the starting point for the domain of the combined function is the set of all values common to both original domains. This common set is known as the intersection of their domains.
Common Domain = Domain($f$) $\cap$ Domain($g$)
For addition, subtraction, and multiplication, this intersection is the final domain of the new function. For division, we have one extra rule to apply.
1. Addition of Two Functions
The sum of two functions, denoted $(f + g)$, is a new function created by adding the outputs of $f$ and $g$ for each valid input $x$.
Definition
The function $(f + g)$ is defined by the rule:
$(f + g)(x) = f(x) + g(x)$
... (1)
Domain
The domain of $(f + g)$ is the set of all $x$ values for which both $f(x)$ and $g(x)$ are defined. This is the intersection of their individual domains.
Domain$(f+g)$ = Domain($f$) $\cap$ Domain($g$).
2. Subtraction of Two Functions
The difference of two functions, denoted $(f - g)$, is a new function created by subtracting the output of $g$ from the output of $f$ for each valid input $x$.
Definition
The function $(f - g)$ is defined by the rule:
$(f - g)(x) = f(x) - g(x)$
... (2)
Domain
Similar to addition, the domain of $(f - g)$ is the intersection of the domains of $f$ and $g$.
Domain$(f-g)$ = Domain($f$) $\cap$ Domain($g$).
3. Multiplication by a Scalar
We can create a new function by multiplying a function $f$ by a constant real number (a scalar), say $c$. This operation, denoted $(cf)$, scales the output of the original function.
Definition
The function $(cf)$ is defined by the rule:
$(cf)(x) = c \cdot f(x)$
... (3)
Domain
A scalar $c$ can be thought of as a constant function $h(x)=c$, whose domain is all real numbers, $\mathbb{R}$. The domain of $(cf)$ is the intersection of the domains of $f$ and $h$. Since Domain($f$) $\cap \mathbb{R}$ is just Domain($f$), the domain remains unchanged.
Domain$(cf)$ = Domain($f$).
4. Multiplication of Two Functions
The product of two functions, denoted $(fg)$, is a new function created by multiplying the outputs of $f$ and $g$ for each valid input $x$.
Definition
The function $(fg)$ is defined by the rule:
$(fg)(x) = f(x) \cdot g(x)$
... (4)
Domain
The domain of $(fg)$ is the intersection of the domains of $f$ and $g$.
Domain$(fg)$ = Domain($f$) $\cap$ Domain($g$).
5. Division of Two Functions
The quotient of two functions, denoted $(f/g)$, is a new function created by dividing the output of $f$ by the output of $g$. This operation has an important extra condition.
Definition
The function $(f/g)$ is defined by the rule:
$\left( \frac{f}{g} \right)(x) = \frac{f(x)}{g(x)}$
... (5)
Domain
The domain begins with the intersection of the domains of $f$ and $g$. However, since division by zero is undefined, we must also exclude any $x$ value from this common domain that makes the denominator function, $g(x)$, equal to zero.
The domain of $\left( \frac{f}{g} \right)$ is therefore defined as:
Domain$\left( \frac{f}{g} \right)$ = $\{ x \in \text{Domain}(f) \cap \text{Domain}(g) : g(x) \neq 0 \}$
Example 1. Let $f(x) = x^2$ and $g(x) = 2x + 1$. Find $(f+g)(x)$, $(f-g)(x)$, $(fg)(x)$, and $\left( \frac{f}{g} \right)(x)$. Also, find their domains.
Answer:
Given:
We are given two real functions:
$f(x) = x^2$
$g(x) = 2x + 1$
To Find:
1. The expressions for the sum, difference, product, and quotient of $f$ and $g$.
2. The domains for each of these new functions.
Solution:
Step 1: Determine individual domains and their intersection.
$f(x) = x^2$ is a polynomial function, so its domain is all real numbers.
Domain($f$) $= \mathbb{R}$
$g(x) = 2x + 1$ is also a polynomial (linear) function, so its domain is all real numbers.
Domain($g$) $= \mathbb{R}$
The intersection of these domains is:
Domain($f$) $\cap$ Domain($g$) = $\mathbb{R} \cap \mathbb{R} = \mathbb{R}$
This common domain, $\mathbb{R}$, is the starting point for all our calculations.
Step 2: Calculate each new function and its domain.
1. Sum of functions $(f + g)(x)$:
$(f + g)(x) = f(x) + g(x) = x^2 + (2x + 1) = x^2 + 2x + 1$
The domain is the intersection of the original domains.
Domain$(f+g)$ $= \mathbb{R}$
2. Difference of functions $(f - g)(x)$:
$(f - g)(x) = f(x) - g(x) = x^2 - (2x + 1) = x^2 - 2x - 1$
The domain is the intersection of the original domains.
Domain$(f-g)$ $= \mathbb{R}$
3. Product of functions $(fg)(x)$:
$(fg)(x) = f(x) \cdot g(x) = x^2(2x + 1) = 2x^3 + x^2$
The domain is the intersection of the original domains.
Domain$(fg)$ $= \mathbb{R}$
4. Quotient of functions $\left( \frac{f}{g} \right)(x)$:
$\left( \frac{f}{g} \right)(x) = \frac{f(x)}{g(x)} = \frac{x^2}{2x + 1}$
For the domain, we start with the common domain $\mathbb{R}$ and exclude values of $x$ where the denominator $g(x) = 0$.
Set the denominator to zero and solve:
$g(x) = 0$
$2x + 1 = 0$
$2x = -1$
$x = -\frac{1}{2}$
We must exclude $x = -1/2$ from the domain.
Domain$\left( \frac{f}{g} \right)$ $= \{ x \in \mathbb{R} : x \neq -\frac{1}{2} \} = \mathbb{R} - \{-\frac{1}{2}\}$
Summary of Results:
- $(f+g)(x) = x^2 + 2x + 1$, Domain: $\mathbb{R}$
- $(f-g)(x) = x^2 - 2x - 1$, Domain: $\mathbb{R}$
- $(fg)(x) = 2x^3 + x^2$, Domain: $\mathbb{R}$
- $\left( \frac{f}{g} \right)(x) = \frac{x^2}{2x + 1}$, Domain: $\mathbb{R} - \{-\frac{1}{2}\}$

